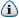|
Hinnavaatlus
:: Foorum
:: Uudised
:: Ärifoorumid
:: HV F1 ennustusvõistlus
:: Pangalink
:: Telekavad
:: HV toote otsing
|
|
| autor |
|
Elof
HV Guru

liitunud: 07.05.2003
|
 12.05.2005 14:54:23
12.05.2005 14:54:23
|

|
|
Need kes kahtlevad asjas seal ikka asja järele proovisid ?
Või on seegi üks suur konspiratsioon ? 
|
|
| Kommentaarid: 212 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 2 :: 2 :: |
 0 :: 0 :: |
 175 175 |
|
| tagasi üles |
|
 |
Marduuhin
HV Guru

liitunud: 02.09.2004
|
 12.05.2005 14:55:37
12.05.2005 14:55:37
|

|
|
| TanElofJ kirjutas: |
Need kes kahtlevad asjas seal ikka asja järele proovisid ?
Või on seegi üks suur konspiratsioon ?  |
Jah proovisin seal. Aga ikkagi kahtlane. Lõpus on ju 2 ust. See eelmine uks ei mõjuta enam midagi. Ja kui 2 ust, siis on ju võiduvõimalus nagu 50:50
_________________
Eesti õigekeelsussõnaraamat ÕS 2018 |
|
| Kommentaarid: 128 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 1 :: 1 :: |
 2 :: 2 :: |
 108 108 |
|
| tagasi üles |
|
 |
M.m.M
HV vaatleja
liitunud: 15.06.2004
|
 12.05.2005 14:58:26
12.05.2005 14:58:26
|

|
|
Kuidas sul sellest nii raske aru on saada?
Kogu tõenäosus selgitatakse juba su esimese otsusega ära. See, mis pärast toimub, ei oma mingit tähtsust. Kõik selgitab ära su algne valik. Ja seal on sul võimalus võita 2/3, sest on kaks võiduta ust ja üks võiduga uks ja tõenäosus et sa valid võiduta ukse on 2/3. Kui sa oled võiduta ukse valinud, siis ei loe enam midagi, sest siis sa oled juba võitnud, kuna saatejuht peab eemaldama teise võiduta ukse ja vahetades oma otsust saad sa võiduga ukse. Kui sa valid alguses võiduga ukse, siis oled sa kaotanud, sest vahetades jääd sa oma võidust ilma. Tõenäosus vahetades võita on 2/3 ja nii see ka jääb.
|
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 15 15 |
|
| tagasi üles |
|
 |
voyager_est
HV Guru

liitunud: 02.11.2002

|
 12.05.2005 15:04:56
12.05.2005 15:04:56
|

|
|
| M.m.M kirjutas: |
Kuidas sul sellest nii raske aru on saada?
Kogu tõenäosus selgitatakse juba su esimese otsusega ära. See, mis pärast toimub, ei oma mingit tähtsust. Kõik selgitab ära su algne valik. Ja seal on sul võimalus võita 2/3, sest on kaks võiduta ust ja üks võiduga uks ja tõenäosus et sa valid võiduta ukse on 2/3. Kui sa oled võiduta ukse valinud, siis ei loe enam midagi, sest siis sa oled juba võitnud, kuna saatejuht peab eemaldama teise võiduta ukse ja vahetades oma otsust saad sa võiduga ukse. Kui sa valid alguses võiduga ukse, siis oled sa kaotanud, sest vahetades jääd sa oma võidust ilma. Tõenäosus vahetades võita on 2/3 ja nii see ka jääb. |
Sa oled vist lolliks joonud ennast ...
Mõtle palun enne, kui kirjutama hakkad.
update:
Loe teema esimene postitus mõttega läbi !
Keegi ei käsi mängijal peale esialgset valikut oma otsust muuta, ta võib algsele valikule kindlaks jääda.
|
|
| Kommentaarid: 74 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 66 66 |
|
| tagasi üles |
|
 |
DoS
HV veteran

liitunud: 18.08.2002
|
 12.05.2005 15:23:59
12.05.2005 15:23:59
|

|
|
| voyager_est kirjutas: |
| See, et alguses kaks võiduta ja üks võiduga uks on, ei mõjuta lõpptulemust. |
Mõjutab, ja kuidas veel. Mõtle nüüd ise hoolikalt.
On olemas 2 erijuhtu: esimene, kui mängija ei vaheta oma esialgset valikut ja teine, kui ta vahetab. Mõlemal juhul saab leida võitmise tõenäosuse kasutades absoluutselt loogilist arutluskäiku:
Vaatleme järgnevalt kõiki neid olukordi, kui mängija vahetab oma esialgse valiku ära.
1) 1/3 juhtudest valib mängija kohe alguses õige ukse. Nüüd avab mängujuht ühe võiduta ukse ja kui mängija vahetab oma esialgse valiku välja, siis võidab ta tõenäosusega 0%.
2) 2/3 juhtudest valib mängija alguses vale ukse. Mängujuht on nüüd igal juhul sunnitud teise vale ukse avama. Kui mängija vahetab esialgse valiku, siis ta võidab 100%.
Kui uks vahetada, siis on võitmise tõenäosus 0*1/3+100*2/3=66%=2/3
Vaatleme nüüd kõiki neid olukordi, kui mängija ei vaheta esialgset valikut.
1) 1/3 juhtudest valib mängija õige ukse. Mängujuht näitab ühe võiduta ukse ette. Kui mängija oma otsust ei muuda, siis võidab ta tõenäosusega 100%.
2) 2/3 juhtudest valib mängija alguses vale ukse. Mängujuht on sunnitud teise vale ette näitama ja kui otsust ei muudeta, siis võidab mängija tõenäosusega 0%
Kui ust mitte vahetada, on võitmise tõenäosus seega 100*1/3+0*2/3=33%=1/3
Ja lõpuks midagi ka 50-50 pooldajatele. Kui mängijad ei tea, et vahetades võidavad nad suurema tõenäosusega, siis umbkaudu pooled mängijad vahetavad otsust ja pooled ei vaheta. Sel juhul on tõenäosus, et saade peab auhinna väljastama (1/2)*(1/3)+(1/2)*(2/3)=1/6+2/6=3/6=1/2 
|
|
| Kommentaarid: 50 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 47 47 |
|
| tagasi üles |
|
 |
voyager_est
HV Guru

liitunud: 02.11.2002

|
 12.05.2005 15:24:58
12.05.2005 15:24:58
|

|
|
DoS, esimene valik ei mõjuta teist.
Teist valikut tehes on valijal alati valida võiduga ja võiduga ukse vahel.
Sest alati võetakse üks võiduta uks ära.
Ja lõplik valik tuleb teha võiduga ja võiduta ukse vahel. Siit tulebki tõenäosus 50:50
UPDATE: Ärge uskuge seda, mida ma siin postituses kirjutasin.
Selle teema ~102. postituses ma sain ka tõenäosuseks 66,6(6) %
viimati muutis voyager_est 12.05.2005 17:44:28, muudetud 1 kord |
|
| Kommentaarid: 74 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 66 66 |
|
| tagasi üles |
|
 |
DoS
HV veteran

liitunud: 18.08.2002
|
 12.05.2005 15:31:20
12.05.2005 15:31:20
|

|
|
| voyager_est kirjutas: |
DoS, esimene valik ei mõjuta teist.
Teist valikut tehes on valijal alati valida võiduga ja võiduga ukse vahel.
Sest alati võetakse üks võiduta uks ära.
Ja lõplik valik tuleb teha võiduga ja võiduta ukse vahel. Siit tulebki tõenäosus 50:50 |
Esialgne valik mõjutab saatejuhi valikut ukse eemaldamisel. Osadel juhtudel on tal võimalus valida, teistel juhtudel on ta sunnitud kindla ukse avama! Seega on need sündmused üksteist mõjutavad.
Aga üldiselt, sina räägid aiast ja mina aiaaugust. Selle 50% jutu ma selgitasin ära juba.
50% võidab tüüp, kes tuleb ja teab, et ühe ukse taga on auhind ja teise taga pole. See mängija aga kes teab ka lisatingimusi, võidab 66% juhtudest.
|
|
| Kommentaarid: 50 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 47 47 |
|
| tagasi üles |
|
 |
voyager_est
HV Guru

liitunud: 02.11.2002

|
 12.05.2005 15:38:51
12.05.2005 15:38:51
|

|
|
| DoS kirjutas: |
| voyager_est kirjutas: |
DoS, esimene valik ei mõjuta teist.
Teist valikut tehes on valijal alati valida võiduga ja võiduga ukse vahel.
Sest alati võetakse üks võiduta uks ära.
Ja lõplik valik tuleb teha võiduga ja võiduta ukse vahel. Siit tulebki tõenäosus 50:50 |
Esialgne valik mõjutab saatejuhi valikut ukse eemaldamisel. Osadel juhtudel on tal võimalus valida, teistel juhtudel on ta sunnitud kindla ukse avama! Seega on need sündmused üksteist mõjutavad.
Aga üldiselt, sina räägid aiast ja mina aiaaugust. Selle 50% jutu ma selgitasin ära juba.
50% võidab tüüp, kes tuleb ja teab, et ühe ukse taga on auhind ja teise taga pole. See mängija aga kes teab ka lisatingimusi, võidab 66% juhtudest. |
Tõenäosuse seisukohalt pole vahet, kumma "tühja" ukse saatejuht eraldab.
Ta võib eraldada ühe kahest alles jäänust tühjast, kui mängija valib esimeses ringis võiduga ukse.
Ja võib eraldada ainsa alles jäänud "tühja" kui mängija valib esimeses ringis ka "tühja".
Igal juhul antakse mängijale teises ringis valida ühe "tühja" ja ühe "täis" ukse vahele.
Seega ei mõjuta esimene ring teist - üks kõik, mis esimeses ringis juhtub, teises ringis on valikuvõimalus 50:50.
Mängujuht ju teab võidu asukohta, temal pole kunagi probleemi "tühja" eraldada.
Mõlemad "tühjad" on ju tõenäosusteooria kohaselt ekvivalentsed.
Pole vahet, kumb "tühi" välja langeb ja kumb teise ringi läheb. "tuhi" on "tühi"
UPDATE: Ärge uskuge seda, mida ma siin postituses kirjutasin.
Selle teema ~102. postituses ma sain ka tõenäosuseks 66,6(6) %
viimati muutis voyager_est 12.05.2005 17:44:54, muudetud 1 kord |
|
| Kommentaarid: 74 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 66 66 |
|
| tagasi üles |
|
 |
pealuu
HV veteran

liitunud: 07.02.2004

|
 12.05.2005 15:49:20
12.05.2005 15:49:20
|

|
|
kui mul antakse võimalus mängida näiteks 100 korda seda mängu (mida ma kahtlen et õnnestub mul teha), siis vahetan alati ust.
kui mul on võimalus mängida vaid üks kord, siis ma ei unusta et ka matemaatiline tõenäosus 1/3 võib olla võitev, mitte kindlasti kaotav ja sisuliselt on mu võimalus 1/2 (pean valima 2 ukse vahel ja üks kord - auto kas: 1. on ukse taga; või 2.ei ole.).
minugipoolest võib alguses olla kasvõi 10 ust (1 võiduga, 9 võiduta) ja siis lastakse mul valida (peale iga valimist avatakse üks võiduta uks) niikaua kuni alles jääb 2 ust. ühe mänguvõimaluse korral on mul lõpuks ikkagi valida 2 ukse vahel.
viimati muutis pealuu 12.05.2005 15:54:31, muudetud 1 kord |
|
| Kommentaarid: 211 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 170 170 |
|
| tagasi üles |
|
 |
Ho Ho
HV Guru

liitunud: 16.02.2002
|
 12.05.2005 15:52:38
12.05.2005 15:52:38
|

|
|
| pealuu, kui sul on näiteks kaks erinevat lotot kus mõlemas on peaauind 1M eeku. Ühe loto puhul on (hüpoteetiline ja mitte kuidagi reaalelule vastav) tõenäosus 1/100, teisel 1/1000 siis kumma loto pileti sa võtad? Nende uste valimistega on sama lugu, tasub teha seda mis on tõenäosem.
|
|
| Kommentaarid: 106 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 1 :: 1 :: |
 86 86 |
|
| tagasi üles |
|
 |
voyager_est
HV Guru

liitunud: 02.11.2002

|
 12.05.2005 16:01:32
12.05.2005 16:01:32
|

|
|
| Ho Ho kirjutas: |
| pealuu, kui sul on näiteks kaks erinevat lotot kus mõlemas on peaauind 1M eeku. Ühe loto puhul on (hüpoteetiline ja mitte kuidagi reaalelule vastav) tõenäosus 1/100, teisel 1/1000 siis kumma loto pileti sa võtad? Nende uste valimistega on sama lugu, tasub teha seda mis on tõenäosem. |
Mina võtaks loomulikult 1/100 võiduvõimaluse.
Aga algse probleemi eripära on selles, et mängija ei saa tõenäosusega võita.
Kõikides võimalikes olukordades, mis võivad tulla, on tõenäosus fifty-fifty.
Mängijast ei sõltu sittagi. Mängujuhist ei sõltu sittagi. Võidu asukohastei sõltu sittagi.
Riigikorrast ei sõltu sittagi. Ilmast ei sõltu sittagi. Mängija soost ei sõltu sittagi.
Mängijal lihtsalt kas joppab või ei joppa. Kas valib teises ringis õige ukse või ei.
Võidu ja kaotuse võimalus on pooleks.
NB! esimese ringi valikule teises ringis kindlaks jäämine on matemaatilise tõenäosusteooria
seisukohalt ka valik teises ringis - mängija valib esimese ringi valiku.
UPDATE: Ärge uskuge seda, mida ma siin postituses kirjutasin.
Selle teema ~102. postituses ma sain ka tõenäosuseks 66,6(6) %
viimati muutis voyager_est 12.05.2005 17:45:11, muudetud 1 kord |
|
| Kommentaarid: 74 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 66 66 |
|
| tagasi üles |
|
 |
pealuu
HV veteran

liitunud: 07.02.2004

|
 12.05.2005 16:12:37
12.05.2005 16:12:37
|

|
|
| Ho Ho kirjutas: |
| pealuu, kui sul on näiteks kaks erinevat lotot kus mõlemas on peaauind 1M eeku. Ühe loto puhul on (hüpoteetiline ja mitte kuidagi reaalelule vastav) tõenäosus 1/100, teisel 1/1000 siis kumma loto pileti sa võtad? Nende uste valimistega on sama lugu, tasub teha seda mis on tõenäosem. |
jah.. kahtlemata tasub teha seda mis on tõenäolisem. kuid kui mul on võimalus mängida 1 kord siis on mul 2 võimalust: 1. lahkun võiduga; 2. lahkun võiduta. milline on tõenäosus?
ma nagu mainisin ka et kui on võimalus näiteks 100 korda mängida siis alati muudaks valikut. seda just tõenäosuse pärast et mitu korda sajast ma võidan (või teisisõnu et mitu korda oli saatejuht sundseisus ukse avamisel).
oluline võib see tõenäosuse asi olla saate tegijatele - kui KÕIK mängijad hakkavad esialgset valikut muutma siis on see neile tõenäosuse põhjal justkui kahjulikum.
ja ka 1/1000 puhul on võimalus et võidan ja 1/100 puhul mitte 
viimati muutis pealuu 12.05.2005 16:14:34, muudetud 1 kord |
|
| Kommentaarid: 211 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 170 170 |
|
| tagasi üles |
|
 |
UMMI9999
HV kasutaja

liitunud: 02.11.2004
|
 12.05.2005 16:13:23
12.05.2005 16:13:23
|

|
|
üritan siis ka seda seletada, et muutes valikut on võiduvõimalus 2/3
xxx - need on 3 ust, millest ühe taga on võit. Uks, mille taga võit on ei mängi praegu rolli.
(x)xx - Oletame, et mängija valib 1. ukse, siis on tema võiduvõimalus 1/3, ning võimalus, et võit on teise kahe ukse taga on 2/3
(x)x[x] - Oletame (jälle), et mängujuht avab peale seda 3. ukse (mille taga pole võitu). Ning kuna me teame, et võimalus, et esimese ukse taga on võit, oli alguses 1/3 ja et võit on 2. või 3. ukse taga on 2/3 saame me sellest järeldada, et valides 2. ukse (ehk muutes valikut) võidame me 2/3 tõenäosusega, kuna uste 2 ja 3 võiduvõimalus oli kokku 2/3 ja kuna me ei saa 3. ust valida, kuna see on juba avatud, on tõenäosus, et 2. ukse taga on võit 2/3
_________________
Quid est veritas?
Kes teab vastust? |
|
| Kommentaarid: 9 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 9 9 |
|
| tagasi üles |
|
 |
M.m.M
HV vaatleja
liitunud: 15.06.2004
|
 12.05.2005 16:18:50
12.05.2005 16:18:50
|

|
|
| voyager_est kirjutas: |
| M.m.M kirjutas: |
Kuidas sul sellest nii raske aru on saada?
Kogu tõenäosus selgitatakse juba su esimese otsusega ära. See, mis pärast toimub, ei oma mingit tähtsust. Kõik selgitab ära su algne valik. Ja seal on sul võimalus võita 2/3, sest on kaks võiduta ust ja üks võiduga uks ja tõenäosus et sa valid võiduta ukse on 2/3. Kui sa oled võiduta ukse valinud, siis ei loe enam midagi, sest siis sa oled juba võitnud, kuna saatejuht peab eemaldama teise võiduta ukse ja vahetades oma otsust saad sa võiduga ukse. Kui sa valid alguses võiduga ukse, siis oled sa kaotanud, sest vahetades jääd sa oma võidust ilma. Tõenäosus vahetades võita on 2/3 ja nii see ka jääb. |
Sa oled vist lolliks joonud ennast ...
Mõtle palun enne, kui kirjutama hakkad.
update:
Loe teema esimene postitus mõttega läbi !
Keegi ei käsi mängijal peale esialgset valikut oma otsust muuta, ta võib algsele valikule kindlaks jääda. |
Ainuke kes ennast lolliks on joonud oled arvatavasti sina.
Algselt seda teemat lugedes olin samuti sinu arvamusel ja olin selles 100% kindel ja mõtlesin vaidlema hakata nagu sina praegu. Aga siis ma lugesin ja mõtlesin veel natuke ja sain asjast aru. Ainuke kes peab mõtlema hakkama oled sina siin, sest sul näib mõistust vähe olevat, kui sa isegi nii lihtsast matemaatikast aru ei saa. Kui sa nüüd oma jonni katki jätaksid ja selge peaga seda veel paarkümmend korda läbi mõtleks, siis võibolla sa saaks ka sellele pihta. Loomulikult ei pea mängija oma otsust vahetama, aga selle teema põhimõte on näidata, et oma otsust vahetades on võiduvõimalus 2/3.
|
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 15 15 |
|
| tagasi üles |
|
 |
Ho Ho
HV Guru

liitunud: 16.02.2002
|
|
| Kommentaarid: 106 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 1 :: 1 :: |
 86 86 |
|
| tagasi üles |
|
 |
pealuu
HV veteran

liitunud: 07.02.2004

|
 12.05.2005 16:19:39
12.05.2005 16:19:39
|

|
|
| UMMI9999 kirjutas: |
üritan siis ka seda seletada, et muutes valikut on võiduvõimalus 2/3
2. ukse (ehk muutes valikut) võidame me 2/3 tõenäosusega, kuna uste 2 ja 3 võiduvõimalus oli kokku 2/3 ja kuna me ei saa 3. ust valida, kuna see on juba avatud, on tõenäosus, et 2. ukse taga on võit 2/3 |
2. ukse taga on ka 1/3 kaotusvõimalust 
|
|
| Kommentaarid: 211 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 170 170 |
|
| tagasi üles |
|
 |
a1
Kreisi kasutaja

liitunud: 25.07.2002
|
 12.05.2005 16:25:29
12.05.2005 16:25:29
|

|
|
tehke väike lihtsustus.
järjekorrast ei sõltu ju midagi, seega muudame järjekorra nii, et esimese ukse taga on võit ja teise ukse taga on kaks ust millest mõlemas on kaotus.
esimeses voorus on seega valikuvõimalus 50:50 võiduga uks või kaotustega uks.
enne teist vooru kõrvaldame ühe kaotusega ukse ja valime jälle kahe ukse vahel suhtega 50:50  
|
|
| Kommentaarid: 39 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 38 38 |
|
| tagasi üles |
|
 |
M.m.M
HV vaatleja
liitunud: 15.06.2004
|
 12.05.2005 16:30:46
12.05.2005 16:30:46
|

|
|
| Sa ei saa lihtsustada ja panna kaht kaotusega ust ühe ukse taha, sest siis muutub tõenäosus valida võiduta uks väiksemaks ja kahaneb ka võiduvõimalus.
|
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 15 15 |
|
| tagasi üles |
|
 |
pealuu
HV veteran

liitunud: 07.02.2004

|
 12.05.2005 16:37:01
12.05.2005 16:37:01
|

|
|
kes tõenäosuse protsendi välja arvutamises tugevamad (noh.. tegelikult vähem laisad kui mina)  : :
10 ust, 1 võiduga, 9 võiduta. mängija saab valida 1 ukse. saatejuht avab 8 võiduta ust. mängijal võimalus kas esimesele valikule kindlaks jääda või valikut muuta. kui suur on tõenäosus võita valiku muutmise korral?
kahtlemata kui mängijana valiksin ühe äärmistest ustest ja siis kui 8 mittevõitva ukse puhul jääb kuskile keskele kinnine uks, siis teeks mind see üüüsna kahtlustavaks (selle kahtluse hajutamiseks oleks muidugi kaval teha mäng selline et mängija ja saatejuht kordamööda valivad uksi - saatejuht muidugi alati võiduta ust avades kuni järgi jääb 2 viimast)  aga küsimus oleks tõenäosuse numbri kohta. aga küsimus oleks tõenäosuse numbri kohta.
viimati muutis pealuu 12.05.2005 16:40:46, muudetud 2 korda |
|
| Kommentaarid: 211 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 170 170 |
|
| tagasi üles |
|
 |
M.m.M
HV vaatleja
liitunud: 15.06.2004
|
 12.05.2005 16:38:32
12.05.2005 16:38:32
|

|
|
| pealuu kirjutas: |
kes tõenäosuse protsendi välja arvutamises tugevamad (noh.. tegelikult vähem laisad kui mina)  : :
10 ust, 1 võiduga, 9 võiduta. mängija saab valida 1 ukse. saatejuht avab 8 võiduta ust. mängijal võimalus kas esimesele valikule kindlaks jääda või valikut muuta. kui suur on tõenäosus võita valiku muutmise korral?
kahtlemata kui mängijana valiksin ühe äärmistest ustest ja siis kui 8 mittevõitva ukse puhul jääb kuskile keskele kinnine uks, siis teeks mind see üüüsna kahtlustavaks  aga küsimus oleks tõenäosuse numbri kohta. aga küsimus oleks tõenäosuse numbri kohta. |
Tõenäosus võita on 90%
|
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 15 15 |
|
| tagasi üles |
|
 |
unknown
HV kasutaja
liitunud: 22.04.2004
|
 12.05.2005 16:43:02
12.05.2005 16:43:02
|

|
|
| a1 kirjutas: |
tehke väike lihtsustus.
järjekorrast ei sõltu ju midagi, seega muudame järjekorra nii, et esimese ukse taga on võit ja teise ukse taga on kaks ust millest mõlemas on kaotus.
esimeses voorus on seega valikuvõimalus 50:50 võiduga uks või kaotustega uks.
enne teist vooru kõrvaldame ühe kaotusega ukse ja valime jälle kahe ukse vahel suhtega 50:50   |
Ei ole 50:50, sest uksi on kokku kolm (esimene + kaks teise ukse taga). 
_________________
Parimate soovidega,
unknown |
|
| Kommentaarid: 5 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 1 :: 1 :: |
 3 3 |
|
| tagasi üles |
|
 |
kvedel
HV vaatleja
liitunud: 27.07.2004
|
 12.05.2005 16:44:12
12.05.2005 16:44:12
|

|
|
Kujutan siis graafiliselt ka, et edaspidi sel ammu selgeks tehtud teemal vähem vaidlusi oleks
Õ tähistab õiget, V valet ust

Nagu siis jooniselt näha on vahetades poole suurem tõenäosus õige ukse taga lõpetada.
|
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 14 14 |
|
| tagasi üles |
|
 |
pealuu
HV veteran

liitunud: 07.02.2004

|
 12.05.2005 16:47:28
12.05.2005 16:47:28
|

|
|
| M.m.M kirjutas: |
| pealuu kirjutas: |
kes tõenäosuse protsendi välja arvutamises tugevamad (noh.. tegelikult vähem laisad kui mina)  : :
10 ust, 1 võiduga, 9 võiduta. mängija saab valida 1 ukse. saatejuht avab 8 võiduta ust. mängijal võimalus kas esimesele valikule kindlaks jääda või valikut muuta. kui suur on tõenäosus võita valiku muutmise korral? |
Tõenäosus võita on 90% |
sellisel juhul võin ma mõttes ka seda algset mängu "modifitseerida" et saada meelepärane karmilt suur tõenäosus võita. kuigi mõlemil juhul oleks mul valida lõpus siiski 2 ukse vahel (sinna viimase 2 ukseni jõudmine on mul garanteeritud).
täpsustuseks ütlen, et mul on võimalus mängida 1 kord vaid.
PS eelmise posti joonise pealt on mu meelest puudu saatejuhi "vale" ukse eemaldamine... vist
|
|
| Kommentaarid: 211 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 170 170 |
|
| tagasi üles |
|
 |
M.m.M
HV vaatleja
liitunud: 15.06.2004
|
 12.05.2005 16:47:58
12.05.2005 16:47:58
|

|
|
| pealuu kirjutas: |
| M.m.M kirjutas: |
| pealuu kirjutas: |
kes tõenäosuse protsendi välja arvutamises tugevamad (noh.. tegelikult vähem laisad kui mina)  : :
10 ust, 1 võiduga, 9 võiduta. mängija saab valida 1 ukse. saatejuht avab 8 võiduta ust. mängijal võimalus kas esimesele valikule kindlaks jääda või valikut muuta. kui suur on tõenäosus võita valiku muutmise korral? |
Tõenäosus võita on 90% |
sellisel juhul võin ma mõttes ka seda algset mängu "modifitseerida" et saada meelepärane karmilt suur tõenäosus võita. kuigi mõlemil juhul oleks mul valida lõpus siiski 2 ukse vahel (sinna viimase 2 ukseni jõudmine on mul garanteeritud).
täpsustuseks ütlen, et mul on võimalus mängida 1 kord vaid. |
Kes siin midagi modifitseerinud on?
Kui oleks 100 ust ja mängujuht avaks 98 valet ust, siis oleks vahetades tõenäosus võita 99%. Ja see tõenäosus on alati, ei loe kas sa mängid seda üks kord või rohkem.
|
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 15 15 |
|
| tagasi üles |
|
 |
Ohohh
Kreisi kasutaja

liitunud: 13.09.2003
|
 12.05.2005 16:49:44
12.05.2005 16:49:44
|

|
|
| voyager_est kirjutas: |
Aga algse probleemi eripära on selles, et mängija ei saa tõenäosusega võita.
Kõikides võimalikes olukordades, mis võivad tulla, on tõenäosus fifty-fifty.
Mängijast ei sõltu sittagi. Mängujuhist ei sõltu sittagi. Võidu asukohastei sõltu sittagi.
Riigikorrast ei sõltu sittagi. Ilmast ei sõltu sittagi. Mängija soost ei sõltu sittagi.
Mängijal lihtsalt kas joppab või ei joppa. Kas valib teises ringis õige ukse või ei.
Võidu ja kaotuse võimalus on pooleks.
NB! esimese ringi valikule teises ringis kindlaks jäämine on matemaatilise tõenäosusteooria
seisukohalt ka valik teises ringis - mängija valib esimese ringi valiku. |
Kuidas ei sõltu. Saatejuhi valik sõltub otseselt mängija esimesest valikust, kuna seda ust ei saa saatejuht reeglite järgi avada. Ja kuna ülejäänud kahest ukseset valib saatejuht vale, siis ta mõjutab otseselt teist valiku vooru.
Kui sa ikka keeldud aru saamast, siis võid ju ise katsetada. Võta 3 kaardi lehte. Näiteks poti äss ja kaks suvalist kaarti. Nüüd veereta täringut, et määrata millise "ukse" valis mängija (näiteks 1,2 esimene, 3,4 teine ja 5,6 kolmas uks). Ise ole saatejuhi eest ja ava üks vale uks. Nüüd hakka üles kirjutama, millal tuli rohkem võite, kas vahetades või mitte.
3 katsest ei piisa. Tee vähemalt 30.
Võin kihla vedada, et varsti saab vojager_est ülesandest aru, siis jäetakse teema mõneks ajaks rahule ja siis tuleb juba keegi uus, kes hakkab jälle kangekaelselt kuulutama, et kõik senised tõestused on jamad ja võiduvõimalus on 50-50
|
|
| Kommentaarid: 6 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 6 6 |
|
| tagasi üles |
|
 |
|