 praegune kellaaeg 07.02.2026 02:41:06
praegune kellaaeg 07.02.2026 02:41:06 |
|
Hinnavaatlus
:: Foorum
:: Uudised
:: Ärifoorumid
:: HV F1 ennustusvõistlus
:: Pangalink
:: Telekavad
:: HV toote otsing
|
|
| autor |
|
lehm2
Kreisi kasutaja

liitunud: 19.09.2004

|
 03.01.2009 17:49:36
Algoritmide keerukus
03.01.2009 17:49:36
Algoritmide keerukus |

|
|
| mesilased kirjutas: |
| troglodyte kirjutas: |
| Sa pead originaal (hashimata) võtme kaasa andma ja listi peal lihtsalt lineaarse otsingu tegema. |
Suured tänud, nii töötab  Mälu kulub ainult n võrra rohkem ning worstcase time complexity on O(1) asemel O(1+n).... Mälu kulub ainult n võrra rohkem ning worstcase time complexity on O(1) asemel O(1+n).... |
Üks offtopic, et kuidas worstcase time complexity määratakse ? O , O(n^2), O(2^n), O(n log n) jne. Ehk oskab maakeeli keegi hästi selgitust anda ? , O(n^2), O(2^n), O(n log n) jne. Ehk oskab maakeeli keegi hästi selgitust anda ? 
_________________
Piilu siia, progreja!
Vajad abi Node.JS-ga ?
Võta ühendust ! |
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 13 13 |
|
| tagasi üles |
|
 |
nene
Kreisi kasutaja

liitunud: 20.03.2004
|
 03.01.2009 20:20:54
03.01.2009 20:20:54
|

|
|
| lehm2 kirjutas: |
| kuidas worstcase time complexity määratakse? |
Raske vastata. Mis sulle täpsemalt segadust valmistab?
|
|
| Kommentaarid: 24 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 1 :: 1 :: |
 23 23 |
|
| tagasi üles |
|
 |
lehm2
Kreisi kasutaja

liitunud: 19.09.2004

|
 03.01.2009 23:29:03
03.01.2009 23:29:03
|

|
|
Näiteks on linear search algoritm, kuidas määratakse time complexity ?
_________________
Piilu siia, progreja!
Vajad abi Node.JS-ga ?
Võta ühendust ! |
|
| Kommentaarid: 15 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 13 13 |
|
| tagasi üles |
|
 |
nene
Kreisi kasutaja

liitunud: 20.03.2004
|
 04.01.2009 17:10:16
04.01.2009 17:10:16
|

|
|
Noh, lineaarse otsingu algoritm on midagi sellist, eksole:
function find(item, array) {
for (i=0; i < array.length; i++) {
if (array[i] == item) {
return i; // item was found, return position
}
}
return -1; // item was not found
} |
Ajalist keerukust saab määrata sedasi, et loed kokku, mitu sammu peab arvuti selles koodis tegema, et tulemuseni jõuda. Lihtsuse mõttes võib lihtsalt kokku arvata kui mitu rida peab läbi käima.
Parimal juhul on otsitav väärtus on massiivis kohe esimesel kohal ja meil pole tarvis ülejäänud massiivi elemente üldse puutuma minna.
Sellisel juhul lõpetab programm oma töö esimese nelja rea läbimisel:
function find(item, array) {
for (i=0; i < array.length; i++) {
if (array[i] == item) {
return i; |
Seejuures on huvitav, et kui otsitav on massiivi alguses, siis ükskõik kui palju elemente meie massiivis ka pole, läbitakse programmi täitmisel alati täpselt neli rida. Seda nimetatakse konstantseks keerukuseks - ükskõik kui palju meil ka sisendandmeid pole, kulub vastuse andmiseks täpselt sama palju aega.
Seega parimal juhul on meie algoritm konstantse keerukusega ehk O(1). Täpsemalt küll O(4), aga oluline on, et keerukus on konstantne, mitte milline see täpne konstant on, seega reeglina kirjutatakse alati lihtsalt O(1).
Halvimal juhtul on otsitav väärtus aga massiivi lõpus ja selle sealt üles leidmiseks peame käima läbi kogu massiivi.
Näiteks kui meie massiivis on 3 elementi, siis tuleb läbi käjja 12 rida:
function find(item, array) {
for (i=0; 0 < array.length; i++) {
if (array[0] == item) {
}
}
for (i=0; 1 < array.length; i++) {
if (array[1] == item) {
}
}
for (i=0; 2 < array.length; i++) {
if (array[2] == item) {
return 2; |
Kui massiivis on aga 10 elementi, siis tuleb läbi käjja tervelt 40 rida:
function find(item, array) {
for (i=0; 0 < array.length; i++) {
if (array[0] == item) {
}
}
for (i=0; 1 < array.length; i++) {
if (array[1] == item) {
}
}
for (i=0; 2 < array.length; i++) {
if (array[2] == item) {
}
}
for (i=0; 3 < array.length; i++) {
if (array[3] == item) {
}
}
for (i=0; 4 < array.length; i++) {
if (array[4] == item) {
}
}
for (i=0; 5 < array.length; i++) {
if (array[5] == item) {
}
}
for (i=0; 6 < array.length; i++) {
if (array[6] == item) {
}
}
for (i=0; 7 < array.length; i++) {
if (array[7] == item) {
}
}
for (i=0; 8 < array.length; i++) {
if (array[8] == item) {
}
}
for (i=0; 9 < array.length; i++) {
if (array[9] == item) {
return 9; |
Nagu näha, siis mida pikem on massiiv, seda rohkem ridu tuleb halvimal juhul läbi käjja. Täpsemalt kui massiivi pikkus on n, siis läbikäidavate ridade arv on 4 * n.
Halvimal juhul on meie algoritm seega lineaarse keerukusega - 10 korda rohkem andmeid võtab 10 korda rohkem aega. Ehk siis O(n). Jällegi võiks öelda et O(4n), kuid oluline on, et keerukus on lineaarne ja kordajad ei muuda asja.
Kõikse olulisem on aga keskmine juhtum. Võime arvestada, et kõige harilikumal juhul ei satu otsitav väärtus mitte massiivi lõppu ega algusesse vaid hoopis keskele.
Näiteks kui massiivis pikkusega 9 asub otsitav väärtus 5. kohal (keskel), siis tuleb selle otsimisel läbida 20 rida:
function find(item, array) {
for (i=0; 0 < array.length; i++) {
if (array[0] == item) {
}
}
for (i=0; 1 < array.length; i++) {
if (array[1] == item) {
}
}
for (i=0; 2 < array.length; i++) {
if (array[2] == item) {
}
}
for (i=0; 3 < array.length; i++) {
if (array[3] == item) {
}
}
for (i=0; 4 < array.length; i++) {
if (array[4] == item) {
return 4; |
Seega läbitavate ridade arv = (n + 1) * 2
Jällegi on tegemist lineaarse keerukusega, kuna 10 korda pikema massiivi puhul kulub taas 10 korda rohkem aega. Ehk siis taas O(n).
Vast oli sest seletusest abi...
|
|
| Kommentaarid: 24 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 1 :: 1 :: |
 23 23 |
|
| tagasi üles |
|
 |
guest1902
Kreisi kasutaja

liitunud: 05.11.2005
|
 04.01.2009 18:18:41
04.01.2009 18:18:41
|

|
|
OT jube, aga mille järgi nad kõike neid algoritme arvutavad? Näiteks ühe kasutu algoritmi jaoks leitigi vist see (alamosa logaritmijunnist)? Ja kas alati määrab see O programmi kiiruse.? Mingine worst case space complexity on kah veel 
|
|
| Kommentaarid: 2 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 2 2 |
|
| tagasi üles |
|
 |
nene
Kreisi kasutaja

liitunud: 20.03.2004
|
 04.01.2009 18:58:19
04.01.2009 18:58:19
|

|
|
| Elrak kirjutas: |
| mille järgi nad kõike neid algoritme arvutavad? |
Ega tegelikult ei arvutagi. Praktikas sul lihtsalt tekib sisetunnetus ühe või teise koodijupi keerukuse kohta.
| Elrak kirjutas: |
| kas alati määrab see O programmi kiiruse? |
Oluline on vaid nende koodijuppide keerukus, mis töötlevad suuremaid andmehulki. Kui sul on tarvis otsida mõnesaja asja seast, siis toimib lineaarne otsing silmapilkselt, kui aga miljardi asja seast, siis lootusetult aeglaselt. Enamiku asjade puhul on lineaarne keerukus OK.
| Elrak kirjutas: |
Mingine worst case space complexity on kah veel  |
Ruumiline keerukus näitab seda, kui palju mälu algoritm võtab. Üldiselt valitseb ajalise ja ruumilise keerukuse vahel teatav tradeoff - kiiremad algoritmid vajavad tavaliselt rohkem mälu. Heaks näiteks on cache kasutamine.
|
|
| Kommentaarid: 24 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 1 :: 1 :: |
 23 23 |
|
| tagasi üles |
|
 |
guest1902
Kreisi kasutaja

liitunud: 05.11.2005
|
|
| Kommentaarid: 2 loe/lisa |
Kasutajad arvavad: |
   |
:: |
 0 :: 0 :: |
 0 :: 0 :: |
 2 2 |
|
| tagasi üles |
|
 |
|
| lisa lemmikuks |
|
 |
sa ei või postitada uusi teemasid siia foorumisse
sa ei või vastata selle foorumi teemadele
sa ei või muuta oma postitusi selles foorumis
sa ei või kustutada oma postitusi selles foorumis
sa ei või vastata küsitlustele selles foorumis
sa ei saa lisada manuseid selles foorumis
sa võid manuseid alla laadida selles foorumis
|
|
Hinnavaatlus ei vastuta foorumis tehtud postituste eest.
|


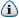






 , O(n^2), O(2^n), O(n log n) jne. Ehk oskab maakeeli keegi hästi selgitust anda ?
, O(n^2), O(2^n), O(n log n) jne. Ehk oskab maakeeli keegi hästi selgitust anda ?